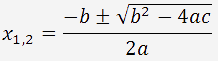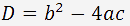Quadratische Gleichungen lösen

Rechner zum Lösen von quadratischen Gleichungen mit reellen und komplexen Lösungen

Quadratische Gleichung Rechner löst quadratische Gleichungen der Form ax² + bx + c = 0, ax² + bx = 0 und ax² + c = 0. Im Einstellungen Fenster stehen verschiedene eingebaute Formate zur Auswahl, z. B. "ax^2 + bx + c = 0", "ax^2 + bx = 0" oder "ax^2 + c = 0". Klicken Sie einfach auf den Pfeil neben dem Feld Formate, und wählen Sie ein beliebiges Format aus.

Um eine quadratische Gleichung zu lösen, geben Sie die Koeffizienten 'a', 'b', 'c' und klicken Sie dann auf 'Lösen'. Dieser Rechner löst quadratische Gleichungen mit gebrochenen Koeffizienten. Die Lösungen können reell aber auch komplex sein.

Der Rechner berechnet die Diskriminante und die Lösungen einer quadratischen Gleichung mit der a-b-c-Formel (Mitternachtsformel).

Was ist eine quadratische Gleichung

Der allgemeine Eintrag einer quadratischen Gleichung ist:
ax² + bx + c = 0
wobei x die Unbekannte ist; a, b und c Koeffizienten aus dem Bereich der reellen Zahlen sind, a ≠ 0.

Formen der quadratischen Gleichung:
ax² + bx + c = 0 ist eine allgemeine quadratische Gleichung.

Eine quadratische Gleichungen, wo b = 0 ist, nennen wir eine quadratische Gleichung ohne das lineare Glied ax² + c = 0.

Eine quadratische Gleichungen, wo c = 0 ist, ist eine quadratische Gleichung ohne das konstante Glied ax² + bx = 0.

Quadratische Gleichung in Normalform, wo a = 1 ist x² + bx + c = 0.

Wenn a=0 ist, ist die Gleichung linear.

Wie löst man eine quadratische Gleichung

Die Formel zur Berechnung der Wurzeln einer quadratischen Gleichung:



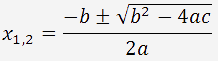
Die Berechnung der Diskriminante einer quadratischen Gleichung


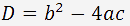
Die Diskriminante kann positiv, gleich Null oder negativ sein:

Wenn die Diskriminante positiv ist (b²-4ac > 0), hat die quadratische Gleichung zwei verschiedene reelle Wurzeln.

Ergibt sich, dass die Diskriminante gleich Null ist (b²-4ac = 0), hat die quadratische Gleichung eine reelle Wurzel.

Ist die Diskriminante negativ (b²-4ac < 0), hat die quadratische Gleichung keine reelle Wurzeln, sondern zwei komplexe Wurzeln.