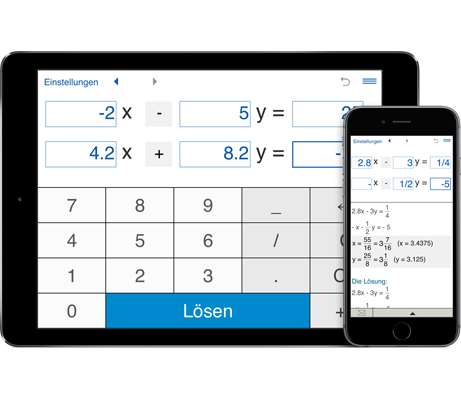
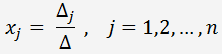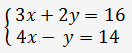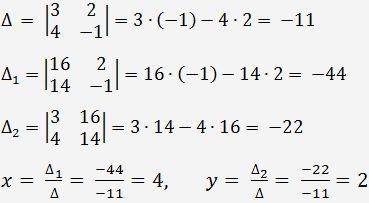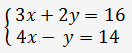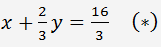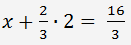Rechner zum Lösen linearer Gleichungssysteme mit 2 Variablen
Das Gleichungssystem zweier linearer Gleichungen mit zwei Unbekannten (2x2 LGS):
a
11x
1 + a
12x
2 = b
1
a
21x
1 + a
22x
2 = b
2
wobei x
1 und x
2 Unbekannt sind;
a
11, a
12, a
21, a
22 die Koeffizienten des Gleichungssystems;
b
1 und b
2 konstante Glieder des Gleichungssystems sind.
Um das Gleichungssystem von zwei Gleichungen mit zwei Unbekannten (2x2 LGS) mit dem Rechner zu lösen, geben Sie einfach die Koeffizienten der Gleichung ein und drücken Sie auf "Lösen".
Lösen der linearen Gleichungen (Cramersche Regel)
Die Cramersche Regel wird zum Lösen linearer Gleichungssysteme mit einer regulären Matrix verwendet. Eine Reguläre Matrix ist eine quadratische Matrix, für die Determinante von Null verschieden ist.
Wir betrachten ein lineares Gleichungssystem n mit Unbekannten x
1, x
2, ..., x
n:
a
11x
1 + a
12x
2 + ...+ a
1nx
n = b
1
a
21x
1 + a
22x
2 + ...+ a
2nx
n = b
2
... ... ... ... ...
a
n1x
1 + a
n2x
2 + ...+ a
nnx
n = b
n
Koeffizientenmatrix ist eine quadratische Matrix, weil sie n Zeilen und n Spalten hat. Lassen Sie uns die Determinante einer Matrix des linearen Gleichungssystems:
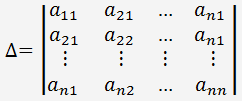
Lassen Sie uns
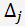
als die Determinante einer Matrix des linearen Gleichungssystems, in dem die j- Spalte durch die Spalte der rechten Seiten des Gleichungssystems ersetzt wird.
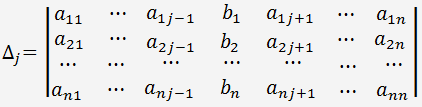
Wenn die System-Matrix-Determinante ungleich Null ist
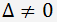
, ist die Matrix regulär und das System hat eine Lösung, für die gilt:
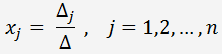
Cramersche Regel ist für ein Gleichungssystem mit zwei und drei Gleichungen geeignet, da die Berechnung der Determinanten der vierten und höheren Ordnung ein aufwändiger Prozess ist.
Wir lösen das folgende Gleichungssystem mit Hilfe der Cramersche Regel.
Betrachten wir ein Gleichungssystem mit zwei linearen Gleichungen mit zwei Unbekannten
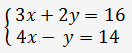
Da die Determinante einer Matrix des Gleichungssystems ungleich Null ist, können Sie die Cramersche Regel anwenden.
Nach der Cramerschen Regel
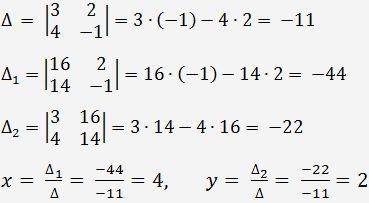
Lösen des linearen Gleichungssystems (Gaußsches Eliminationsverfahren)
Das Lösungsprinzip der linearer Gleichungssysteme mit dem Gaußschen Eliminationsverfahren basiert auf der sukzessiven Elimination der Gleichungssysteme durch elementare Zeilenumformungen auf Zeilenstufenform, die dem ursprünglichen Gleichungssystem entspricht und schließlich dann die Suche nach der Lösung des Gleichungssystems durch Rücksubstitution.
Das Lösen des Gleichungssystems mit zwei linearen Gleichungen mit zwei Unbekannten mit Hilfe der Gaußschen Eliminationsverfahren
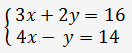
Wir dividieren die ersten Gleichungssysteme durch 3
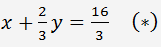
Wir multiplizieren (*) mit 4 und subtrahieren es von der zweiten Gleichung. Wir erhalten das folgende Gleichungssystem.

Dies ergibt die Lösung y = 2. In der ersten Zeile ersetzen wir es für 'y' und lösen 'x'.
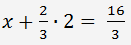
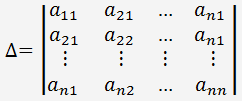
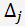 als die Determinante einer Matrix des linearen Gleichungssystems, in dem die j- Spalte durch die Spalte der rechten Seiten des Gleichungssystems ersetzt wird.
als die Determinante einer Matrix des linearen Gleichungssystems, in dem die j- Spalte durch die Spalte der rechten Seiten des Gleichungssystems ersetzt wird.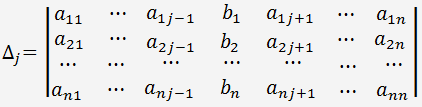
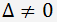 , ist die Matrix regulär und das System hat eine Lösung, für die gilt:
, ist die Matrix regulär und das System hat eine Lösung, für die gilt: