Lösen linearer Gleichungssysteme mit drei Variablen
Rechner zum Lösen linearer Gleichungssysteme mit 3 Variablen
Das Gleichungssystem dreier linearer Gleichungen mit drei Variablen (3x3 LGS):
a
11x
1 + a
12x
2 + a
13x
3 = b
1
a
21x
1 + a
22x
2 + a
23x
3 = b
2
a
31x
1 + a
32x
2 + a
33x
3 = b
3
x
1, x
2 und x
3 Unbekannt sind;
a
11,..., a
33 die Koeffizienten der Gleichung sind;
b
1, b
2 ubd b
3 konstante Glieder des Gleichungssystems sind.
Um das Lineare Gleichungssysteme mit drei Variablen lösen, geben Sie einfach die Koeffizienten der Gleichungen ein und tippen Sie auf Lösen.
Die Cramersche Regel zur Lösung linearer Gleichungssysteme
Die Berechnung der Wurzeln eines Gleichungssystems von linearen Gleichungen von Cramersche Regel ist nützlich für Systeme von zwei und drei Gleichungen, da die Berechnung der Determinanten des vierten und höheren Ordnungen ist recht umständlich. Die Cramersche Regel wird zum Lösen linearer Gleichungssysteme mit n Variablen mit einer regulären Matrix verwendet. Eine Reguläre Matrix ist eine quadratische Matrix, für die Determinante von Null verschieden ist.
Wenn die Cramersche Regel nicht anwendbar ist, können wir lösen das Gleichungssystem mit Gaußsches Eliminationsverfahren.
Betrachten wir ein Gleichungssystem von n Gleichungen mit n Variablen x
1, x
2, ..., x
n:
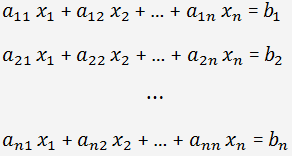
Die Cramersche Regel darf nur für n x n Systeme von linearen Gleichungen angewendet werden, wenn die Determinante der Koeffizientenmatrix ungleich Null ist.
Die Determinante einer Koeffizientenmatrix des linearen Gleichungssystems:
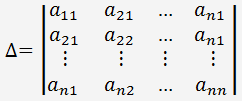
Bezeichnen
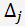
als die Determinante einer Matrix des linearen Gleichungssystems, gebildet durch Ersetzen des j-ten Spalte der rechten Seite Spalte Gleichungen.
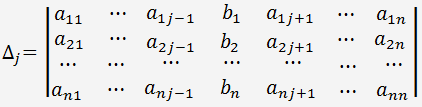
Wenn die Determinante ungleich Null ist, das System hat eine Lösung.
Von Cramersche Regel:
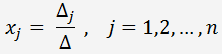
Das Lösen des Gleichungssystems von 3 Gleichungen mit 3 Variablen mit Hilfe der Gaußschen Eliminationsverfahrenn
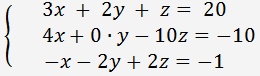
Wir dividieren die ersten Gleichungssysteme durch 3
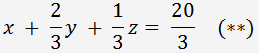
Wir multiplizieren (**) mit 4 und subtrahieren es von der zweiten Gleichung, dann multiplizieren die Gleichung (**) mit -1 und subtrahieren es von der dritte Gleichung. Wir erhalten das folgende Gleichungssystem.
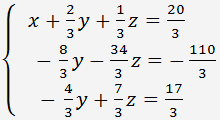
Wir dividieren der zweiten Gleichung
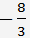
und erhalten
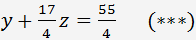
Wir multiplizieren die Gleichung (***)
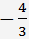
und subtrahieren es von der dritte Gleichung. Wir haben die folgenden System von Gleichungen
![]()
Aus der letzten Gleichung finden wir z=3. Setzt man das Ergebnis in die zweite Gleichung:
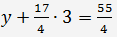
=> y=1.
Setzt man y und z in die erste Gleichung und finden x
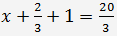
=> x=5.

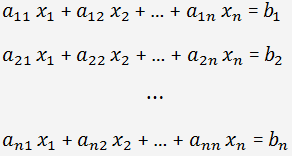
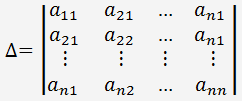
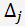 als die Determinante einer Matrix des linearen Gleichungssystems, gebildet durch Ersetzen des j-ten Spalte der rechten Seite Spalte Gleichungen.
als die Determinante einer Matrix des linearen Gleichungssystems, gebildet durch Ersetzen des j-ten Spalte der rechten Seite Spalte Gleichungen.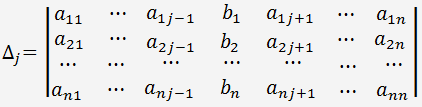
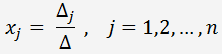
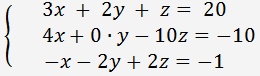
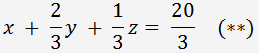
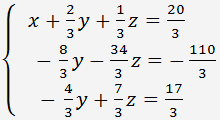
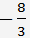 und erhalten
und erhalten 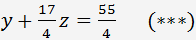
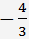 und subtrahieren es von der dritte Gleichung. Wir haben die folgenden System von Gleichungen
und subtrahieren es von der dritte Gleichung. Wir haben die folgenden System von Gleichungen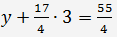 => y=1.
=> y=1.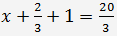 => x=5.
=> x=5.