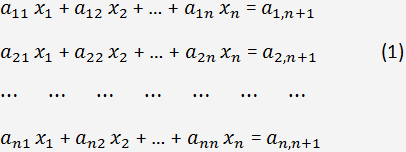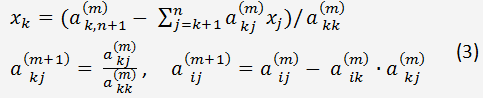Rechner für Lineare Gleichungssysteme

Lineare Gleichungssysteme lösen

Rechner für lineare Gleichungssysteme mit zwei und mehr Unbekannten

Rechner zum Lösen linearer Gleichungssysteme mit N Gleichungen und N Variablen 2x2 3x3 4x4 5x5 6x6 7x7 8x8 9x9 10x10 11x11.

Dieser Rechner löst lineare Gleichungssysteme bis zu 11 Unbekannte: lineare Gleichungssysteme mit 2 Gleichungen und 2 Unbekannten (2x2 LGS), lineare Gleichungssysteme mit 3 Gleichungen und 3 Unbekannten (3x3 LGS), lineare Gleichungssysteme mit 4 Unbekannten (4x4 LGS), lineare Gleichungssysteme mit 5 Unbekannten (5x5 LGS), lineare Gleichungssysteme mit 6 Variablen (6x6 LGS), lineare Gleichungssysteme mit 7 Variablen (7x7 LGS), lineare Gleichungssysteme mit 8 Variablen (8x8 LGS), usw.

Um das Gleichungssystem zu lösen, geben Sie die Anzahl der Gleichungen und die Koeffizienten der Gleichung ein und drücken Sie "Lösen".

Lösen von linearen Gleichungssystemen (Gaußsches Eliminierungsverfahren)

Das Lösen der Gleichungssysteme unter Verwendung Determinanten sollte auf Gleichungssysteme mit 2 und 3 Gleichungen durchgeführt werden.

Für größere Anzahl von Gleichungen ist viel besser Gaußsche Eliminationsverfahren verwenden.

Betrachten Sie das lineare Gleichungssystem:



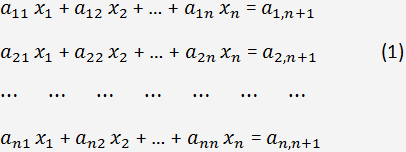
wobei x_i sind unbekannt, i = 1, 2,..., n; n < 200. Wenn die Anzahl der Gleichungen von mehr als 200, ist es notwendig, Iterationsverfahren zur Lösung.
a_i,j - sind die Elemente der erweiterten Matrix von Koeffizienten.

Vorwärtselimination
In Übereinstimmung mit der Gaußschen Eliminationsverfahren finden x₁ aus der ersten Gleichung

x₁ = (a_1,n+1 - a_1,2x₂ - ... - a_1nx_n)/a₁₁     (2)
Wenn a_1,1 = 0, und es ist ein von Null verschiedenes Element in der ersten Spalte, sollten wir tauschen Zeilen. Dann ersetzen (2) in alle Gleichungen des Gleichungssysteme (1), mit Ausnahme der ersten Gleichung. Somit wird, das unbekannte x₁ aus allen Gleichungen, mit Ausnahme der ersten Gleichung, eliminiert werden. Die Elemente der erweiterten Matrix werden durch die Formeln umgewandelt:

a_1j⁽¹⁾ = a_1j/a₁₁

a_ij⁽¹⁾ = a_ij - a_i1a_1j⁽¹⁾, i = 2,3,...,n; j = 1, 2,..., n+1
Nach Beseitigung x₁ aus allen Gleichungen, sind alle Elemente der ersten Spalte der transformierten Matrix gleich Null, außer a₁₁⁽¹⁾ = 1

Wiederholen Sie diesen Vorgang für x₂. In ähnlicher Weise drücken x₂ aus der zweiten Gleichung und eliminieren sie vom Rest der Gleichungen, usw.
Wir erhalten die transformierte Matrix, in der alle Elemente unterhalb der Hauptdiagonalen sind Null.
Schreiben die entsprechenden Formeln für den Ausschluss von unbekannten x_k und erhalten Koeffizienten der transformierten Matrix.


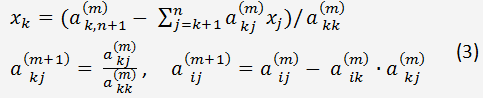Rückwärtseinsetzen oder Rücksubstitution
Nun können wir bestimmen, alle Unbekannten x_k, beginnend mit x_n und endend mit x₁.