Kubische Gleichungen lösen
Rechner zum Lösen von kubischen Gleichungen
Dieser Rechner löst kubische, quadratische und lineare Gleichungen, einschließlich Gleichungen mit Brüchen und Klammern. Der Rechner für kubische Gleichungen löst nicht Gleichungen mit x im Nenner (Bruchungleichungen).
Vordefinierte Format zum Lösen von Gleichungen dritten Grades der Formen ax
3 + bx
2 + cx + d - 0 mit Hilfe der Cardanischen Formel. Um die Wurzeln einer kubischen Gleichung zu finden, geben Sie die numerischen Koeffizienten 'a', 'b', 'c', 'd', und klicken Sie auf "Lösen". Die Koeffizienten 'a', 'b', 'c', 'd', sind reelle Zahlen, a ≠ 0.
Das Lösen einer kubischen Gleichung
Eine allgemeine kubische Gleichung (Gleichung dritten Grades) hat die folgende Form:
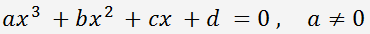
Das Lösen einer kubischen Gleichung - die Lösungsformel für kubische Gleichungen (Cardanischen Formel).
Wie löst man eine kubische Gleichung mit Hilfe der Cardanischen Formel.
Nach der Division der Gleichung durch die Zahl
a 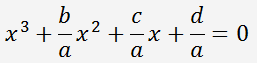
und der Substitution
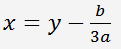
erhalten wir eine reduzierte kubische Gleichung
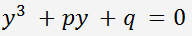
, wo
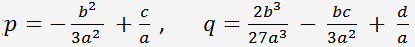
.
Die Lösungsformel für die Berechnung der Wurzeln der kubischen Gleichungen und der Diskriminante:
Die Diskriminante der kubischen Gleichung
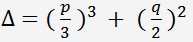
.
Die Lösungsformel für kubische Gleichungen:
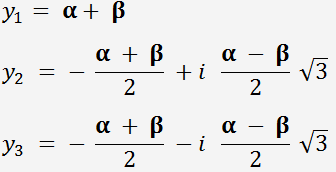
wo
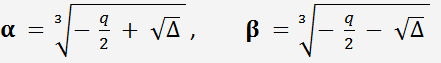
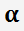
und
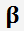
wählen wir so, dass
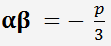
.
Wenn
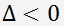
, hat die Gleichung drei reelle Wurzeln.
Wenn
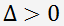
, hat die Gleichung eine reelle Wurzel und zwei verbundene Komplexwurzeln.
Wenn
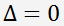
, hat die Gleichung zwei reelle Wurzeln. Wenn p = q = 0 ist, hat die Gleichung eine reelle Wurzel.

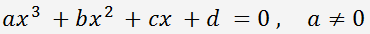
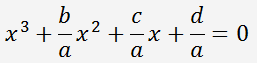 und der Substitution
und der Substitution 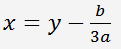
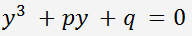 , wo
, wo 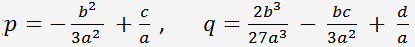 .
.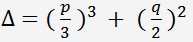 .
.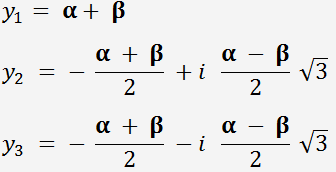
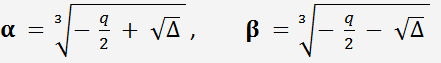
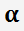 und
und 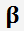 wählen wir so, dass
wählen wir so, dass 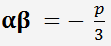 .
.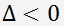 , hat die Gleichung drei reelle Wurzeln.
, hat die Gleichung drei reelle Wurzeln.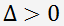 , hat die Gleichung eine reelle Wurzel und zwei verbundene Komplexwurzeln.
, hat die Gleichung eine reelle Wurzel und zwei verbundene Komplexwurzeln.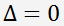 , hat die Gleichung zwei reelle Wurzeln. Wenn p = q = 0 ist, hat die Gleichung eine reelle Wurzel.
, hat die Gleichung zwei reelle Wurzeln. Wenn p = q = 0 ist, hat die Gleichung eine reelle Wurzel.